The Prisoner's Dilemma

Imagine this: two prisoners are being prepared for a long session of interrogation, both prisoners are in separate rooms and have no idea what the other prisoner is going to say. They have been presented with three options.

1. To remain silent and not say anything, resulting in only a one-year jail sentence each.
2. But if either confesses the truth, the one who remains silent would have to serve five years in jail, and the other would be set free.
3. And if they both confess, they each receive three years of jail time.

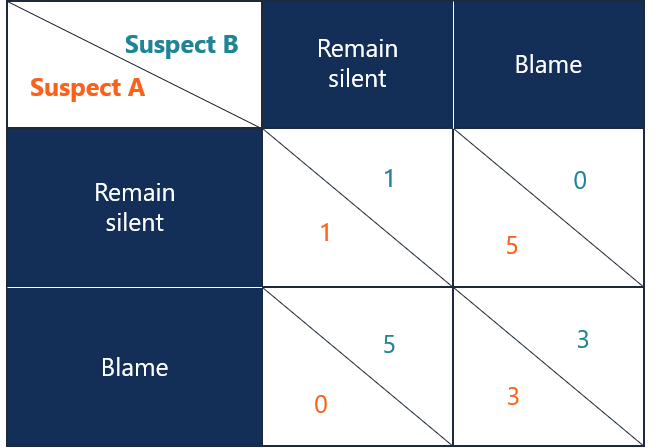
This is called The Prisoner's Dilemma. This is a famous game in game theory. It illustrates why two rational players might confess even if that does not lead to the best possible outcome for them.

Considering this from a rational perspective, the best option for both is to remain silent for the whole interrogation to minimize their jail time. However, they can’t risk it all in the hope that the other person will not confess too, in which case they might have to suffer the consequences of receiving a longer sentence.

If they really trust each other and work as a team that would help them get less period of sentence. But what if they do not trust each other?

This takes us to “Nash equilibrium” where both players confess, resulting in 3-year sentences each. But why would they choose that?

Choosing to confess means they will either receive a three-year sentence each or be released with no time at all, both of which are better than one of them facing a five-year sentence alone.

The concept was first proposed by John Forbes Nash Jr in 1950, in his doctoral dissertation “Non-Cooperative Games”. And shows how rational individual choices can lead to collective outcomes that are worse for everyone.

In a single shot game like the prisoner's dilemma, where the stakes are high, people often choose to defect. But what about repetitive games? Is it still the best strategy when players interact multiple times?

The Iterated Prisoner’s Dilemma

The Iterated Prisoner’s Dilemma (IPD) is a repeated version of the classic Prisoner’s Dilemma, a game theory scenario that explores cooperation and defection. Unlike one-off games, repeated games allow players to develop strategies that account for future consequences, making reputations and trust essential factors.

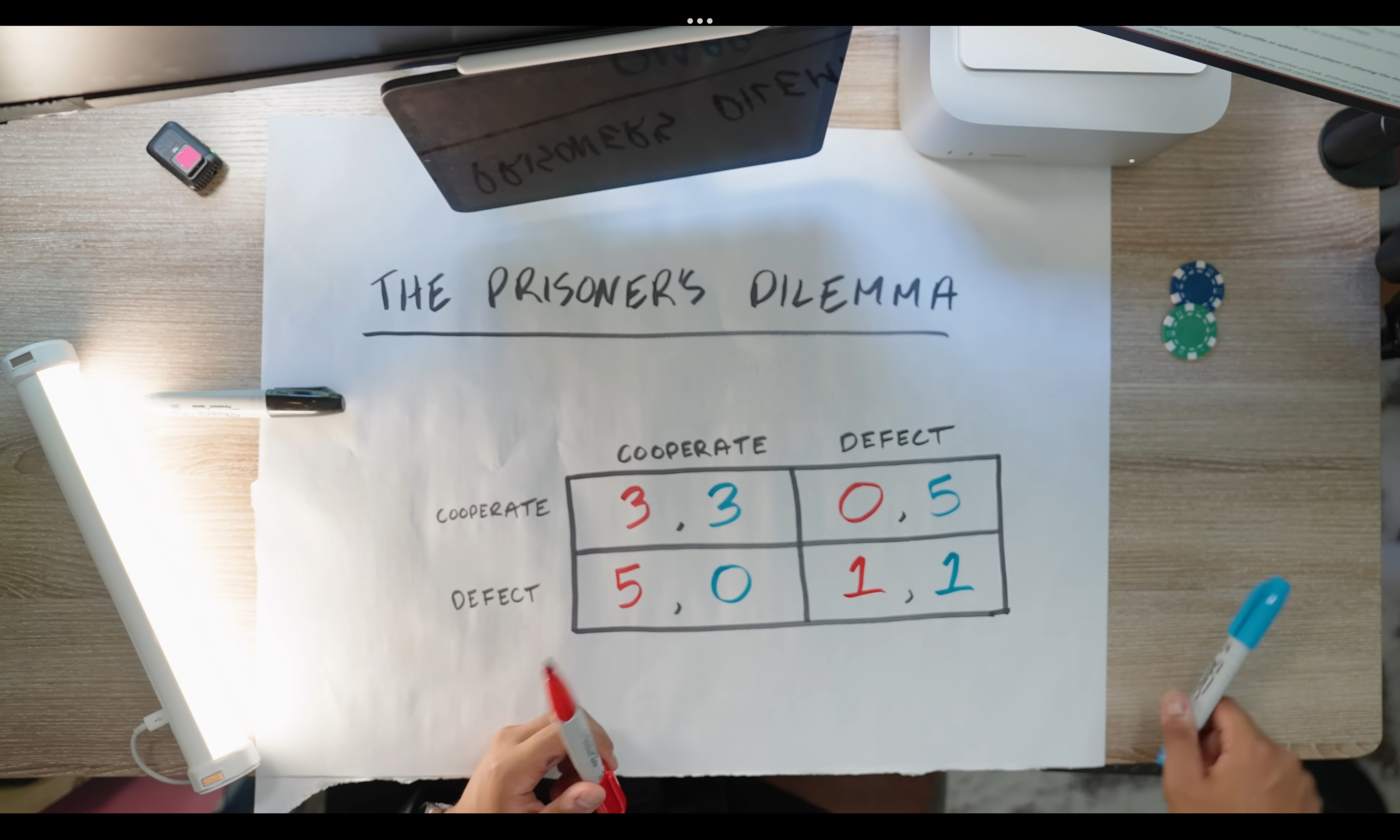
Two players can either cooperate (C) or defect (D). The payoffs are structured as follows:

1. If both of them decided to co-operate they will get 3 points each.
2. If one of them decided to defect while the other cooperated, the person who cooperated will get 0 points and the other will get 5 points.
3. And if they both defected they will get 1 point each.

In these sorts of repetitive games, players can remember past actions and adjust their strategies based on it. Which makes trust and long-term relationships matter more in Iterated Prisoner’s Dilemma.

But just like a prisoner's dilemma the best option for the players is to cooperate every single time. The Nash equilibrium would also be the same, which is defection.

But we are not rational beings, even if it is better to cooperate every single round, the urge to defect by both people would be higher knowing the person in front of me will cooperate every single time so why not defect and take five points instead of three?

This desire to get more, pushes us as a human to defect and hence makes our choices unpredictable. So what is the strategy for the game as the opponent's choice is unpredictable? It might be cooperate every single time, it could be defect the whole time, or follow some mixed strategy?

In 1980, Robert Axelrod held a tournament where anyone could submit a strategy for an iterated prisoner's dilemma. Each strategy played 200 rounds against each other strategy. There were 14 strategies submitted by the people.

These were the payoffs:

1. If both of them cooperated with each other for all 200 rounds they would get 600 points each.
2. If they both defected they would both get 200.
3. If one cooperated and the other defected the whole time, one would get 0 and the other 1000.
4. If they went back and forth, like this, they would each get 500.

And these are the averaged results of the tournament.

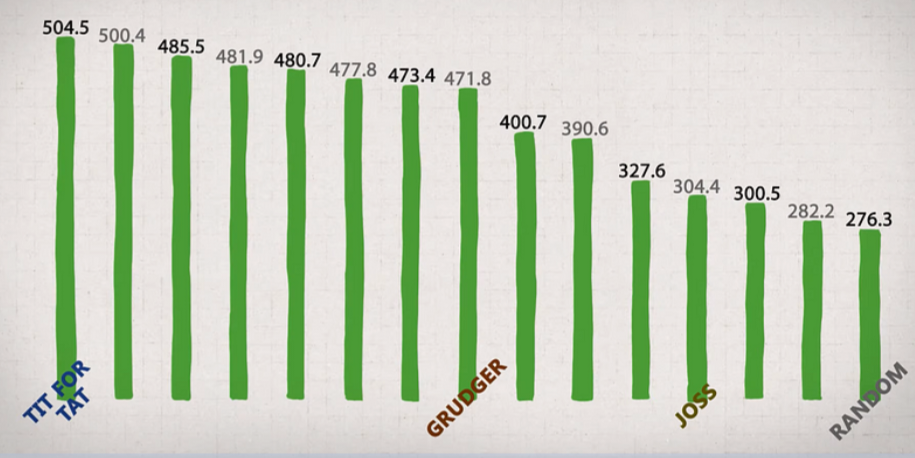
The winner strategy was ‘tit for tat’, the strategy says to co-operate in the first round and then mimic the other player’s previous move. The results showed that this strategy outperformed other strategies of winning due to straightforward approach and an ability to foster cooperation.

Advantages of tit for tat strategy

1. It’s simple and transparent: if you treat me well, I’ll treat you well; if you try to harm me, I’ll respond in the next round. This makes it predictable but fair.
2. Since it retaliates against unfair actions, it prevents others from continuously taking advantage of you.
3. Also it is forgiving, if they try to cooperate further in the game, it changes to cooperate and maintains a good relationship further.
4. Unlike an always-aggressive strategy, tit-for-tat doesn’t escalate conflicts unless provoked, helping to maintain stability.

Since then countless more strategies came but this remains the best!

But how is this relevant in day-to-day life? And most importantly is it even important?

More about Game Theory in next blog. Stay tuned!